Scientists from Japan have proposed a novel approach for finding the best routing paths for vehicles in charge of bicycle rebalancing.
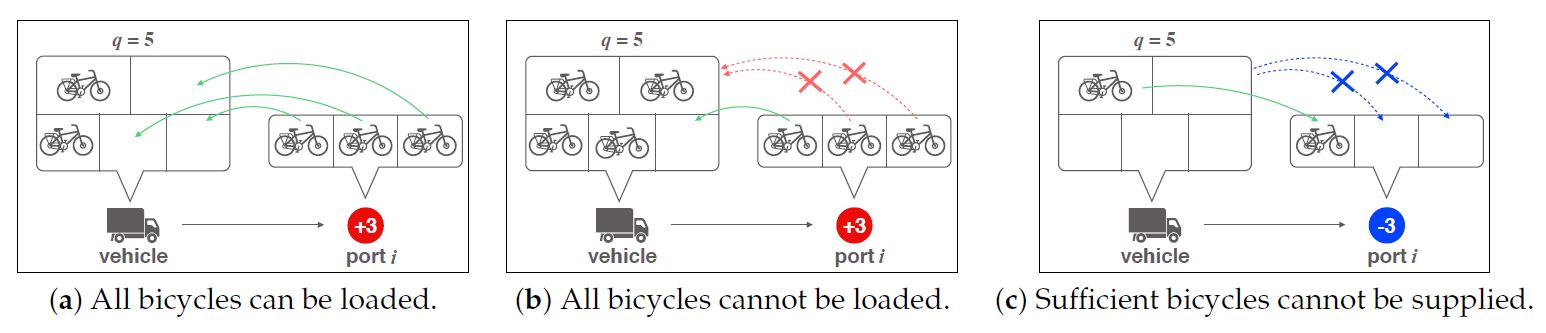
Much research has been dedicated to the bicycle rebalancing problem using a fleet of vehicles. Finding the optimal routing paths for the vehicles is in and of itself a highly complex mathematical problem in the field of combinatorial optimization. One must make sure that the optimization algorithms used can reach a good-enough solution in a reasonable time for a realistically large number of ports and vehicles. Many methods, however, fail to find feasible solutions when multiple constrains are considered simultaneously, such as time, capacity, and loading/unloading constraints for the vehicles (Figure 1).
In a recent study published in MDPI’s Applied Sciences, a team of scientists suggested an innovative twist to the routing problem of bicycle sharing systems using this concept.
Led by Professor Tohru Ikeguchi of Tokyo University of Science, the team comprising PhD student Honami Tsushima from Tokyo University of Science and Associate Professor Takafumi Matsuura from Nippon Institute of Technology, Japan, proposed a new formulation of the routing problem in which the constraints imposed on the routings can be violated. This enabled using the optimization algorithm for exploring what is known as the space of “infeasible solutions.”
Prof. Ikeguchi explains their reasoning, “In real life, if a work can be completed through overtime within a few minutes, we would work beyond the time limit. Similarly, if we are only carrying four bikes and need to supply five, we would still supply the four we have.”
Following this line of thought, the researchers formulated the “soft constraints” variant of the routing problem in bicycle rebalancing. Using this approach, instead of outright excluding solutions that violate constraints, these can be considered valid paths that incur dynamically adjusted penalties and taken into consideration when assessing possible routings. This approach enabled the team to devise an algorithm that can make use of the space of infeasible solutions to speed up the search for optimal or near-optimal solutions.
The researchers evaluated the performance of their method through numerical experiments with benchmark problems including up to 50 ports and three vehicles. The results show that their strategy could find optimal or near-optimal solutions in all cases, and that the algorithm could search both the feasible and infeasible solution spaces efficiently. This paints a brighter future for people in cities with congested traffic in which bicycle sharing systems could become an attractive solution. As Prof. Ikeguchi remarks, “It is likely that bike sharing systems will spread worldwide in the future, and we believe that the routing problem in bicycle rebalancing is an important issue to be solved in modern societies.”
Hopefully, further efforts to improve bicycle sharing systems will alleviate traffic congestion and make people’s lives in big cities healthier and more enjoyable.